It's easy to claim "99.9% uptime", as so many web hosting services do. Just define it as one piece of modern electronic equipment, the server itself, capable of running, even if it isn't connected to the internet.
The practice isn't new. As early as the 1950's, when I first became involved with computers, IBM defined their rental computers' uptime that way. For an entire day every month, the computer was unavailable to its users because IBM was doing monthly maintenance. It was still "up" according to IBM. Even though it took up to half an hour to "reIPL" (IBM lingo for "restart") several times a day, the computer uptime clock was ticking the whole time even though users were ticked off.
To a user, there is only one proper definition of "up": can I use it? Here's how to estimate what that uptime is for viewers of your web pages.
It's based on access logs, maintained by your web page server so they know how much they can charge you for bandwidth and hit costs. You normally have access to them via the same FTP address you use for maintaining your site. They contain entries of the form
75.25.130.254 - - [01/Jan/2008:00:02:11 -0600] "GET /rvwinter.html HTTP/1.1" 200 24570 "-"
"Mozilla/4.0 (compatible; MSIE 7.0; Windows NT 5.1)"
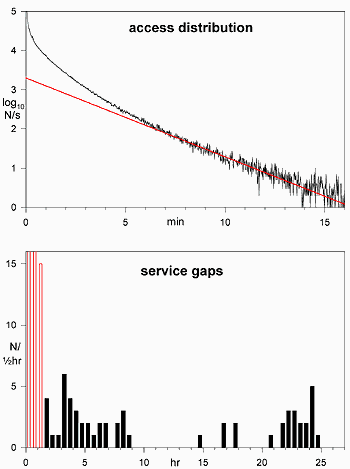To determine uptime, it's the field in square [ ] brackets that's important. Convert
each to a time in seconds from the start of your logs, then analyse the
differences between successive times. Here's what I got from my server,
IX Web Hosting
over three years (1 March 2005-29 February 2008).
The top graph shows the short time scale. The red line on the log-linear plot marks an exponential distribution, the hallmark of events randomly distributed in time. The increase in rate below 5 minutes is due to non-random causes. Most of my pages include images, which are requested as soon as a page is loaded. And, web accelerators load pages refered to by the current page in advance whether they will be actually viewed or not. The random portion of the distribution (the slope of the red line) has an interval of 2.1 minutes, while the overall mean interval is 16 s. So, each random request results in an average of 7 additional non-random requests.
This random distribution must be subtracted from the time interval histogram to identify service gaps. The second graph, based on a longer time scale, shows that it has reached zero by 1.5 hours. The 0.5-1 slot is 494 events, the 1-1.5 slot 15, so the projected contribution of the access distribution to the 1.5-2 hour slot is 0.03 The black events of the lower graph, therefore, mark provable times when people were unable to access my pages. My server may, of course, have been unavailable for shorter periods in addition, but this method can't show them.
Total unavailable-to-viewers time: 664.4 hours over 36 months. Maximum possible viewer up-time: 97.5%. That's the time during which everything necessary was working: not just the host server, but the host routers and host internet access as well.
Of course, the server operator can measure their traffic flow second by second. But, just as in the old days, I don't know of any service provider who makes this statistic available to users. You have to do it yourself.