
NTC Thermistor Theory
As outlined in the previous section, a simple approximation for
the relationship between Resistance and Temperature for an NTC thermistor
assumes an exponential relationship between them. This approximation
is based on simple curve fitting to experimental data and also on
an intuitive feel for electrical behaviour of semiconductor devices.
The exponential approximation is a mathematical model that applies
an equation that can be expressed in the form:
RT = ![]() exp(ß/T)
............ (equation # 4)
exp(ß/T)
............ (equation # 4)
Where:
RT is the Resistance in ohms at temperature
T
T is the absolute Temperature in Kelvin
A is a linear factor
"exp" is the exponential function
ß is the exponential factor known as "beta" value
or sensitivity index of the thermistor material.
The ß value is a very important parameter in the description and specification of thermistor materials and thermistor components. When the natural log of both sides of the equation is taken, the relationship becomes:
ln(RT) = C + ( ß/T) ................. (equation # 5)
Where C is a constant factor, (C = ln(A)) from the equation
above.
If ln(RT) is plotted versus 1/T, (as
in graph #4) then the slope of the resulting curve will be equal
to beta, ß.
This equation provides a reasonable approximation to measured data,
but as mentioned in the previous section, the thermistor materials
are not ideal materials. For the exponential model to apply over
a large temperature range (greater than 50 °C) the beta value
has to vary, therefore the beta value is not constant over extensive
ranges. In fact, the beta value is also temperature dependent
and it decreases with temperature.
Although this simple exponential model for the relationship between Resistance and Temperature of athermistor is limited over large temperature spans, concepts derived from it are of importance in the thermistor industry and in the specification of NTC thermistors. Some of these concepts are developed in the following sections with the intention of explaining some of the basic calculations and specifications used in the industry.
Practical application of the beta value:
It is common practice to specify thermistor materials in terms of
beta value over a particular temperature span.
For a temperature T1 and thermistor resistance R1 at this temperature
T1:
R1 = A exp (ß/ T1).
For a temperature T2 and thermistor resistance R2 at this temperature
T2:
R2 = A exp ((ß/ T2).
Taking the ratio: R1 / R2 = exp(ß(1/ T1 - 1/ T2))
The expression for ß then becomes:
Where:
ß has units of temperature (Kelvin)
"ln" represents the natural logarithm (log base e)
inverse of the exponential function.
In this form, published beta values can be used to calculate
resistance or temperature values when other items in the equation
are known.
The beta value can then be regarded a quantitative value of thermistor
materials that is assigned as a material constant and that indicates
the relationship of material resistivity to temperature.
Application of the beta value is demonstrated in a numerical
example at the end of this section.
The general information on sensitivity of material resistivity to
temperature that can be interpreted from the beta value is indicated
in Graph # 5. This shows the resistivities of BetaTHERM’s
Standard Thermistor Materials versus their 0/50 °C Beta Values.
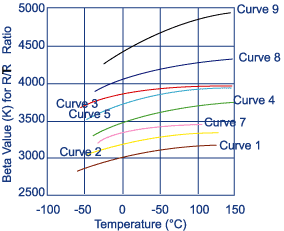
The beta value is derived from a mathematical approximation. For
this mathematical approximation to apply over a large temperature
range, beta has to vary with temperature. This variation of beta
value with temperature is indicated in Graph # 6. The variation
is greater at the low temperature end of the curve. This variation
should be borne in mind when using beta values for calculations
over temperature ranges.
Because the beta value is an indication of the relationship between
the resistivity of thermistor material and temperature, it can also
be used to calculate alpha (a) value (temperature coefficient) for
a thermistor made from the same material. Recalling the definition
of the alpha value as the percentage change in resistance per °C,
given by equation # 3
and, expressing R as a function of T using the exponential model, it can be shown that a good approximation for the temperature coefficient or alpha value, at a temperature T Kelvin, in terms of beta is :
The beta value is a single expression that can be regarded as a
material constant. It depends on basic material properties,
and beta values derived from measurements provide an indication
of general thermistor material quality.
Although deviations in beta value from nominal values affect the
tolerance of thermistors and are indicative of material quality,
such deviations are not widely published by thermistor manufacturers.
Typically, manufacturers will list the nominal Beta Value only or
will list the nominal Beta Value with a tolerance expressed in K.
BetaTHERM provide information on beta value deviations for the range
of thermistor materials that it produces. This information is contained
in Table #2. This lists the beta values and deviations for
high precision BetaCURVE thermistors and includes data for low precision
tolerance BetaCHIP thermistors also.
Graphs of Material resistivity versus Beta value, and Beta Value
versus temperature are included also to illustrate how Beta is regarded
as a material characteristic that is related to resistivity. The
relationship between Beta value and temperature shows the temperature
regions for which Beta value is approximately constant for different
materials.
Sample calculations are included in this section also to illustrate some typical engineering uses of beta values.
| Beta Values and tolerances for
BetaCURVE and BetaCHIP series Thermistors. |
||
| 0/50 Beta Value (K) | ||
| Material Curve # | BetaCURVE | BetaCHIP |
| 1 | 3108 +/-0.40% | 3108 +/-1.7% |
| 2 | 3263 +/-0.38% | 3263 +/-0.9% |
| 3 | 3892 +/-0.32% | 3892 +/-1.0% |
| 4 | 3575 +/-0.30% | 3575 +/-1.0% |
| 5 | 3811 +/-0.33% | 3811 +/-0.9% |
| 6 | 4143 +/-0.30% | 4143 +/-1.3% |
| 7 | 3422 +/-0.36% | 3422 +/-1.0% |
| 9 | 4582 +/-0.63% | 4582 +/-1.9% |
Table # 2
Material Resistivity vs. Beta Value for BetaTHERM Thermistor Materials
(Curves )
 |
Graph # 5
Beta Values vs. temperature for Betatherm Materials
 |
Graph # 6
Examples of calculations using Beta values:
(The 0/50 Beta value means a Beta value calculated from resistance
data at 0°C and at 50°C)
Example: Calculate the 0/50 Beta value for BetaTHERM’s 30K5A1
thermistor, given the following information:
R1 is resistance value measured
at T1, 0°C = 94980 ohms
R2 is resistance value measured
at T2, 50°C= 10969 ohms
The relevant formula for calculating the beta value is:
Where:
ß has units of temperature (Kelvin)
ln represents the natural logarithm (log base e)
inverse of the exponential function.
Temperatures are expressed in Kelvin.
This can then be written as:
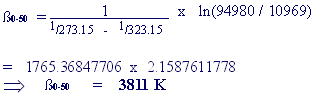 |
Since the Beta value of a thermistor material is derived from an
exponential model, it can also be used to calculate resistance values
of a thermistor at a particular temperature when the resistance
at another temperature is known. This is demonstrated in the following
example:
Example: Calculate the resistance of a BetaTHERM 10K3 thermistor
at 33°C using the following information:
The resistance of the thermistor at 25 °C is 10000 ohms, the
0-50 Beta value is 3892 K
Using the equation:
R1 / R2
= exp(ß (1/ T1 - 1/ T2))
and writing it in the form:
R2 = R1
/ (exp(ß (1/ T1 - 1/ T2)))
where
T1 = 25°C = 298.15 K, R1
= 10000 ohms.
T2 = 33°C = 306.15 K, ß= 3892
K
Using these values, the value of R2 is calculated as:
R2 = 10000 / (exp(0.3411094421367))
Resistance at 33°C calculated using Beta value:
R2 = 7109.81ohms.
The value of resistance
of a 10K3 device
that is published
in the
R /T tables is 7097.2 ohms.
The sensitivity of the resistance of the device to temperature in
this region is 304 ohms per °C. The difference between the published
resistance value and the resistance value that is calculated using
the beta value is equivalent to .04 °C .
Using the Beta 0-50 value in the range 0-50 °C, the maximum
errors are at the ends of the range, and are of the order of 0.22
°C.
When the tolerance of the Beta value is taken into account,
then the errors at the ends of the range for material 3 BetaChip
products are of the order of 0.45°C, while the errors
at the ends of the range for material 3 BetaCurve products
are of the order of 0.29 °C.
| The main purposes of these examples were : | |
| To show some typical uses of Beta values in calculations. | |
| To demonstrate the difference between BetaCHIP and BetaCURVE | |
| product. In particular to show that the tighter tolerance BetaCURVE product has lower errors than the BetaCHIP product in converting from Resistance to temperature using the exponential model. | |
| To establish the relevance of Beta as a material characteristic. | |
| To show some of the limitations of the exponential model | |
| so that further modelling of the R / T characteristics of thermistors can be considered. | |
Further Modelling of NTC Thermistor R/T
Characteristics:
The concepts introduced so far to relate the resistance of a thermistor
to the temperature have been primarily based on the characterization
and specification of materials and on the use of material
parameters rather than on component parameters.
While the temperature coefficient or alpha value can be used to calculate the temperatures corresponding to various resistance values of a thermistor, the method is rather limited. A look-up table of Resistance versus Temperature values for the thermistor is required and details of alpha values at various points are needed also. It is very useful and relevant in certain situations.
The use of Beta Values or sensitivity index, and the associated exponential model are useful for material specification, and for the comparison of the sensitivity of bulk materials. The method is somewhat limited for general use in relating the resistance of a thermistor to temperature over extensive ranges mainly because of the temperature dependence of the Beta Value itself.
In general applications NTC thermistors are used to measure temperature, and this is accomplished by measuring the resistance of the thermistor and then using that resistance value to make an estimate of temperature. The various means of relating resistance of a thermistor to the temperature that have been discussed so far are not ideally suited to this, as outlined above. The requirement is for a single equation that can be used easily to relate resistance and temperature of thermistors. The requirement is all the more important to optimize the use of programmable calculators, computer spreadsheets and microcontrollers.
Because the conduction mechanism in metal oxide semiconductors
is a complex one, it is difficult to explain accurately by applying
mathematics to a physical model. The method used for accurate
mathematical modelling of the Resistance versus Temperature characteristic
of a thermistor is to obtain accurate measurements of Resistance
and Temperature of components and to apply curve fitting techniques
to model the relationship between them.
The next section of this catalog describes the mathematical model,
which is in general use throughout the industry, to give a single
equation that relates the Resistance and Temperature of an NTC thermistor
component. The equation is called the Steinhart-Hart Equation,
and it is used by all thermistor manufacturers.
| North America: | Europe: |
 |
 |
| Tel: 508 842 0516 | Tel: +353 91 753238 |
| Fax: 508 842 0748 | Fax: +353 91 705943 |