Pottery: Glaze Thermal Expansion
Calculating expansion
Strength & rigidity
Comparison of expansion data
Derivation of recommended values
References
Expansion Data Fitting
Making a glaze expansion sample
Calculating expansion
As long as a ceramic melts to form a glass, it is possible to approximate its
thermal expansion with a linear model: the proportion of each oxide is multiplied by
the expansion of that oxide; the sum of these is then a reasonable approximation to
the expansion of the glaze. This method is not applicable to fired clay bodies, as
they don't completely melt; their expansion has to be measured directly.
Hewitt&Bailey provide a list for one manufacturer at
Calculating Crazing.
There have been many tables of oxide thermal expansion published over the years; see
Hewitt&Bailey
for a summary. The oxide constitution of many minerals and frits is at
Digitalfire.
Ron Roy has published the recipes and average measured expansions over 50-600°C of
five glazes in Mastering Cone 6 Glazes,
pp72-81. I currently use the oxide expansion data of Appen, Technology of Enamels because
it's the most complete data available from a primary source. Whichever set you use with
your glaze calculation program, line fit the calculated to actual values, then use the
fit-derived correction. When comparing a glaze expansion to those of my clays using the
Sankey coefficients below, I use
ExpectedExpansion=(CalculatedExpansion*0.81)+0.63 because this is the best fit to Ron Roy's
data and his data is what I have for my clays. However, the best fit with these coefficients
to Hall's data is no correction; the reasons for this discrepancy have not yet been resolved.
If you don't have line fitting software, here is
a method that can be used with a desk calculator.
Calculated glaze expansions must be treated with caution for several reasons:
- The method assumes linearity. The expansions of glazes are not linear
with temperature - see Mastering Cone 6 Glazes,
pp72-81 for some actual expansion curves. Appen, Hall and Gilard&Dubral
tested for linearity due to some oxide concentrations in a glaze
and found rates that varied markedly with concentration for several oxides.
It must be assumed that some of the well known oxide compounds behave differently
than the sum of their parts until proven otherwise. I know of no author
who has investigated the latter; it seems to have been assumed that such
compounds can't occur in a fully melted (glassy) glaze. In the case of
iron silicates, we know they do occur.
-
The measurements were made by adding small amounts of the oxide under test to
a reference glaze, then measuring the difference in expansion compared to the
reference glaze alone. Authors used different reference glazes, different firing
temperatures and different temperature ranges, and the distances involved are
very small. The temperature range of interest to pottery is from the temperature
at which the glaze effectively solidifies during cooling (500°C or higher
for most pottery glazes) to freezer temperature (-15°C). Most authors
measured over a temperature range far smaller than this (English&Turner
25-90°C, Winkelmann&Schott 20-100°C, Mayer&Havas 20-150°C,
Appen 20-400°C, Hall 25-500°C, Ron Roy 50-600°C). Still,
it's a graphic warning of the complexity of the problem when one author
gets a positive value and another a negative, as M&H and Appen did for
ZrO2 and SnO2.
-
Some elements exist in more than one oxide form and it's not always clear
which form is in a glaze. X-ray analysis of
iron glazes indicate that even red glazes
contain large amounts of black FeO, so the difference in expansion of FeO
and Fe2O3 presents an
additional uncertainty.
The procedure for making a glaze expansion sample is described below and shown at
right. Hall made 124! You should appreciate how much work lies behind those numbers
in expansion tables when you wonder why so many authors measured so few oxides.
The coefficients of the two clay bodies I use were measured on the same apparatus
and over the same range as used for the glaze expansions:
Tucker Smooth White
stoneware: 6.64x10-6/K
Tucker 6-50
porcelain: 7.71x10-6/K
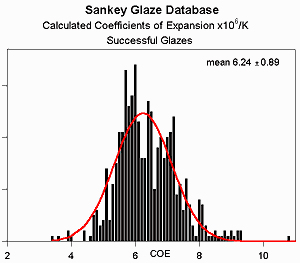 It is generally believed that the expansion for a stable glaze must be 1-10% less than
that of the clay. Glaze expansions much less than this can result in shivering - the
breaking off of sharp pieces of glaze under thermal stress. Glaze expansions higher
than that of the clay can cause crazing - fine cracks in the glaze surface that will
trap contaminants, thus making the item unsuitable for containing food.
It is generally believed that the expansion for a stable glaze must be 1-10% less than
that of the clay. Glaze expansions much less than this can result in shivering - the
breaking off of sharp pieces of glaze under thermal stress. Glaze expansions higher
than that of the clay can cause crazing - fine cracks in the glaze surface that will
trap contaminants, thus making the item unsuitable for containing food.
However, analysis of successful
glazes from the Clayart archives
calls this into question - glazes can have expansions well outside this range and
still be successful. The mean COE of these glazes is
6.2x10-6/K as expected, but the range is far wider than
10%. It should be noted, however, that almost none of the testers
performed any functional tests, such as a freezer to boiling water cycle.
Strength & rigidity
The tensile strength of a glaze affects the fit of glaze to body. A high tensile
strength enables a glaze to withstand a greater mismatch than a low one. Tensile
strength varies inversely with thickness, so the thicker the glaze, the more
likely it is to fail. Hall provides factors for tensile strength which are
useful as a guide to which glaze compositions will be strongest:
| oxide | BaO | SiO2
| Al2O3 | ZnO | PbO
| Na2O | K2O
| B2O3 | CaO | MgO
|
|---|
| factor | 3 | 7 | 12 | 20 | 20 | 20 | 40 | 61 | 70 | 80
|
|---|
| (units are kg/mm2 for rods
0.35-0.5 mm diameter, by weight)
|
The elasticity of a glaze also affects the fit of glaze to body. A low rigidity
(high elasticity) enables a glaze to withstand a greater mismatch than high
rigidity. Hall provides factors for rigidity which are useful as a guide to
which glaze compositions will be the least elastic:
| oxide
| K2O
| Na2O
| SiO2
| BaO
| Al2O3
| ZnO
| PbO
| CaO
| B2O3
| MgO
|
|---|
| factor | 4.3 | 5.3 | 6 | 7.5 | 10 | 10 | 14.5 | 15 | 16 | 19
|
|---|
| (units are g/mm2 for rods
0.8-3 mm diameter, by weight)
|
What is wanted in a glaze is high tensile strength coupled with low rigidity.
Dividing Hall's tensile strength factors by his rigidity factors yields a
dimensionless factor of merit:
| oxide
| BaO
| SiO2
| Al2O3
| PbO
| ZnO
| Na2O
| B2O3
| MgO
| CaO
| K2O
|
|---|
| factor(SiO2=1)
| 0.3 | 1.0 | 1.0 | 1.2 | 1.7 | 3.2 | 3.3 | 3.6 | 4.0 | 8.0
|
|---|
From this data, the most useful oxide to improve the ability of a glaze to
withstand expansion mismatch is K2O, with
CaO, MgO, B2O3 and
Na2O in second rank. They increase the tensile
strength the most and increase the rigidity the least of a glaze containing them.
Comparison of expansion data
Primary sources (those who are believed to have measured the values quoted),
linear expansion x10-6/K:
| molar | | by weight
|
|---|
| oxide | Sankey | Appen | aw | Appen(aw=60) | English & Turner
| Gilard & Dubral | Hall | Mayer & Havas | Winkelmann & Schott
|
|---|
| range(C) | | 20-400 | | 20-400 | 25-90 | ? | 25-500 | 20-150 | 20-100
|
|---|
|
|
| Li2O | 27 | 27 | 29.88
| 54 | | | | | 6.7
|
| Na2O | 39.5 | 39.5 | 61.98 | 38 | 41.
6 | 51
| 38 | | 33
|
| K2O | 46.5 | 46.5 | 94.20
| 30 | 39.0 | 42 | 30 | | 28
|
|
|
| BeO | 4.5 | 4.5 | 25.01 | 10.8 | | | |
15.7
|
| MgO | 3.4 | 6
| 40.31 | 8.9 | 4.5 | 0 | 2 | | 0.3
|
| CaO | 13 | 13 | 56.08 | 14 | 16.3 | 11# | 15 | | 17
|
| MnO | 10.5 | 10.5 | 70.94 | 8.9 | | | | 7.3
|
| FeO | 5.5 | 5.5 | 71.85 | 4.6 | | | |
6.6
|
| NiO | 5 | 5 | 74.69 | 4.0 | | | | 13.3
|
| CoO | 5 | 5 | 74.93 | 4.0 | | | | 14.6
|
| CuO | 3 | 3 | 79.55 | 2.3 | | | | 7.3
|
| ZnO | 5 | 5 | 81.39 | 3.7 | 7.0 | 7.7
| 10 | | 6
|
| SrO | 16 | 16 | 103.62 | 9.3
|
| CdO | toxic | 11.5 | 128.41 | 5.4
|
| BaO | 20 | 20 | 153.33 | 7.8 | 14.0 | 9.1 | 12 | | 10
|
| PbO | toxic | see below | 223.20 | 3.5 | 10.6 | 11.5
| 7.5 | 14 | 10
|
|
|
| SiO2
| 3.8 | see below | 60.09
| 3.8* | 0.5 | 0.4 | 4.0* | | 2.7
|
| TiO2 | see below
| see below | 79.87 | 1.1* | | | | 13.6
|
| ZrO2 | -6 | -6 | 123.22
| -2.9 | 2.3 | | | 7
|
| SnO2 | -4.5 | -4.5 | 150.71
| -1.8 | | | | 6.6
|
| CeO2 | 4.0 |
| 172.12 | | | | | 14
|
|
|
| B2O3
| see below | see below | 69.62 | -5 to 0
| -6.5 | -4 | 2 | | 0.3
|
| Al2O3
| 4.2 | -3 | 101.96 | -1.8 | 1.4 | 2
| 5 | | 17
|
| Mn2O3 | 21 | 21
| 157.88 | 8.0
|
| Cr2O3 |
4.2 | | 151.99 | | | | | 17
|
| Fe2O3 | see below
| 11 | 159.69 | 4.1 | | | | 13.3
|
| Sb2O3 | 7.5
| 7.5 | 285.42 | 1.6
|
|
|
| P2O5
| 14 | 14 | 141.94 | 5.9 | | | | | 6.7
|
| Sb2O5 | | | 323.5
2
| | | | | 8.3 | 6.7
|
* 60% SiO2.
# 10% CaO, all other G&D oxides at 0%.
To use the molar values, divide the weight of each oxide used by its atomic
weight, then normalise the sum to unity (1.0). To use the by-weight values,
normalise the sum of weights of all oxides in the glaze to unity.
 Appen molar formulae for the variable expansion oxides:
Appen molar formulae for the variable expansion oxides:
- PbO: 13 + (50 * (A - 0.03)) where A is the sum
of the molar fractions of
Li2O, Na2O and
K2O
- SiO2: 3.8 for 0-0.67 molar,
3.8 - (10 * (S - 0.67)) for 0.67-1.00
molar where S is the molar fraction of SiO2
- TiO2:
3 - (15 * (S - 0.5))
- B2O3:
(1.25 * (4 - X)) - 5;
to obtain the factor X, add the molar fractions of the five oxides
Li2O, Na2O,
K2O, CaO and BaO then subtract the molar fraction of
Al2O3;
divide the result by the molar fraction of
B2O3. If the result is greater
than 4, X = 4.
Hall's graph for the variable expansion of silica is well fitted by the equation
4.9 + (2.5 * S) - (6.8 * S * S)
where S is the molar fraction of SiO2.
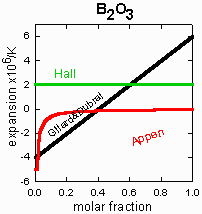
Three authors looked for coefficients that vary with concentration: Hall, Appen, and
Gilard&Dubral. Hall found no dependence for
B2O3, while Appen and
Gilard&Dubral did. I have not yet located the original papers of Appen or
Gilard&Dubral, but the glazes listed below, most of which
are Hall's, do not support any concentration-dependent coefficients.
|
Derivation of recommended values
Appen did not measure Cr2O3.
Since Mayer&Havas did, and both obtained reasonably consistent measurements of CuO,
CoO and NiO (I omit ZrO2 and
SnO2,
where their results were inconsistent) the missing Appen value can be
approximated by proportion. The data of Appen is linear molar, that of M&H cubic
by weight, so it is necessary to determine the
atomic weights
of the comparison oxides to convert between molar and by-weight
measures. The average molar weight of practical glazes is very close to that of
silica, 60, so that's a good reference molar weight to use for intercomparisons.
| oxide | M&H | Appen | AW | ratio(AW=60)
|
|---|
| CuO | 2.2 | 3.0 | 79.55 | 1.05
| | CoO | 4.4 | 5.0 | 74.93 | 0.93
| | NiO | 4.0 | 5.0 | 74.69 | 1.02
| | Cr2O3 | 5.1 | --- |
151.99
|
The mean ratio between the authors' numbers referred to an atomic weight of 60
is 1.00±0.04 (as it should be). So, the linear molar 'Appen' value for
Cr2O3
may be estimated from the cubic by weight of M&H as
5.1/3*1.00*151.99/60 = 4.2x10-6/K.
The same method was used to derive the value for CeO2.
When Hall's formula for the expansion of SiO2 is compared
to Appen's variable formula and to a constant value with the set of glazes listed below,
there is insufficient evidence for a variable coefficient,
so Appen's value is retained. Once this is chosen, the best fit for
Al2O3 is +4.2 (equivalent to
2.5 by weight), in much better agreement with other data than Appen's value of -3.
Following this, the best fit for MgO is 3.4 (5 by weight), also more in agreement with
other results.
X-ray analyses show that almost all of the iron in a glaze
is FeO; Fe2O3 is restricted to
crystals
on the surface. There is evidence that other sesquioxides that also exist in a monoxide
form do the same. I therefore recommend that all oxides that exist in both forms be
converted to monoxide equivalent before calculating expansion or unity values.
References
- Appen: quoted by Vargin, Technology of Enamels (English translation of a Russian text)
- English & Turner: quoted by Hewitt&Bailey from J.Am.Ceram.Soc. 10(8),551
(1927),
Relationship Between Chemical Composition and the Thermal Expansion of Glasses;
ibid. 12,760 (1929) correction
- Gilard & Dubral: quoted by Dodd, Dictionary of Ceramics from Verres
Silicates Ind. 5,122,141 (1934)
- Hall: J.Am.Ceram.Soc. 13(3):182-190 (1930), The Influence
of Chemical Composition on on the Physical Properties of Glazes
- Mayer & Havas: quoted by Singer&German, Ceramic Glazes, and by Vargin
from Sprechsall 42:497; 44:188-207, Coefficient of Expansion of Enamels and their
Chemical Composition
- Winkelmann & Schott: Ann.Physik Chemie 51:730-746(1894), Ueber thermische
Widerstandcoefficienten verschiedener Gläser in ihrer Abhängigkeit von der
chemischen Zusammensetzung
- Hewitt&Bailey quotes Appen's value for
Fe2O3 in Vargin as the full oxide;
Vargin actually says for ½ the oxide.
- Vargin refers to P2O5 as
P2O3.
- Hewitt&Bailey refer to AsO5 which doesn't exist;
Vargin uses As2O3 for the same
entry.
The important oxides for pottery glazes where there is major disgreement are
shown in red. That's where I'll be focussing my studies for now. I plan basically
to correct the molar data of Appen whenever there is clear evidence that he was wrong.
Initial trials of iron, zirconia and tin are in progress.
Expansion Data Fitting
Hall's data is of superb quality. However, little of it can be used by modern
potters. 50% of his test glazes used lead, which no potter can now use. And, of the
remainder that are free of barium and arsenic, most had expansion coefficients
far in excess of that required to fit modern clays. Hesselberth&Roy found
that a glaze expansion of 7.76x10-6/K crazed on all
clays they tested. Only eleven of Hall's non-toxic glazes have lower expansion
than this. Here are the glazes useful to potters that are available for data
fitting:
| molar fractional composition
|
|---|
| # | COE
| SiO2
| Al2O3
| K2O
| Na2O
| CaO
| MgO
| ZnO
| B2O3
| SrO
|
|---|
| H&R1 | 5.40 | .6748 | .0652 | .0072 | .0349 | .1055 | .0466 |
- | .0631 | -
| | H&R2 | 5.78 | .6568 | .0772 | .0171 | .0366 | .1156 | .0359 |
- | .0585 | -
| | H&R3 | 6.36 | .6476 | .0927 | .0294 | .0357 | .1213 | .0248 |
- | .0462 | -
| | H&R4 | 6.89 | .6411 | .0855 | .0377 | .0382 | .1417 | .0103 |
- | .0441 | -
| | H&R5 | 7.56 | .6267 | .0937 | .0291 | .0555 | .1412 | .0006 |
- | .0247 | .0249
| | H68 | 7.9 | .5472 | .0501 | .0012 | .1410 | - | - | - | .2606 | -
| | H88 | 6.4 | .7335 | .1070 | .0255 | .0032 | .1308 | - | - | - | -
| | H91 | 7.8 | .6230 | .0967 | - | .0406 | .2386 | .0011 | - | - | -
| | H92 | 4.7 | .5810 | .1051 | - | .0380 | - | .2759 | - | - | -
| | H93 | 4.9 | .5168 | .1218 | .0008 | .0459 | - | .3147 | - | - | -
| | H98 | 8 | .5622 | .0773 | .0502 | .0742 | - | .1531 | - | .0830 | -
| | H105 | 5.8 | .6591 | .0586 | .0396 | .0256 | - | - | - | .2171 | -
| | H110 | 6.8 | .6197 | .1450 | .0211 | .0115 | .0970 | - | .0794 | .0
263 | -
| | H112 | 7.6 | .6082 | .0735 | .0021 | .1004 | - | .0521 | .0711 | .0
928 | -
| | H113 | 7.2 | .5992 | .0687 | .0007 | .0965 | - | .1041 | .0410 | .0
897 | -
| | H122 | 7.9 | .5810 | .1221 | .0153 | .0163 | .2653 | - | - | - | -
| | H123 | 5.9 | .5471 | .1440 | .0167 | .0229 | .0074 | .2619 | - | -<
td>-
| | H124 | 5.4 | .5595 | .1445 | .0144 | .0189 | .0083 | .2543 | - | -<
td>-
| | H125 | 7.1 | .7093 | .1002 | .0273 | .0295 | .1337 | - | - | - | -
| | H127 | 6.6 | .5690 | .1327 | .0140 | .0164 | .1987 | .0691 | - | -<
td>-
|
H&R: Mastering Cone 6 Glazes, pp72-81.
H: Hall: J.Am.Ceram.Soc. 13(3) pp184-189
The data of Hall and H&R have a serious consistent difference.
The best fit of the Sankey molar coefficients above to H&R's data is
0.81*a+0.63 ±0.02, while the best fit to Hall's is 1.05*a-.07 ±0.1
This requires further investigation.
Making a glaze expansion sample
- Mix a sample of the glaze.
- Cut a firebrick to a suitable size with a hacksaw, then make a roughly rectangular
hole about 3 cm wide, 9 cm long and 5 cm deep. A carbide masonry drill
makes it easy, but a coarse metal file will work.
- Line the hole with clay. Make the layer as thin as possible while still having no
pinholes that would leak. The aim is to have a liquid-tight layer that is more fragile
than the glaze sample so it can be removed after firing without breaking the sample.
- Mix alumina hydrate with 2% Bentonite and moisten with vinegar just enough to allow
mixing. Pure alumina will not be dissolved by the glaze, thus modifying its composition
and therefore its expansion rate. After firing, the alumina will be crumbly enough to be
separated from the sample. The Bentonite and vinegar allows the mixture to stick
together just enough to hold its place in the mould. The clay keeps the moisture in the
alumina mixture from wicking into the brick, so it dries properly.
- Line the mould with the alumina mixture, about 5 mm thick. It can be patted
into place with a piece of wood. The end result should be a space for glaze that is at
least three times as deep as wide, since most glazes shrink to about 50% of their dry
volume when melted, and some of the glaze will soak into the alumina.
- Fill the mould with glaze. Keep topping it up until everything appears dry, then
press a finger firmly in the middle - there will be room for more. An oven at 80°C
speeds this process up. When really full, dry overnight in the oven.
- Glaze fire, holding at maximum temperature for half an hour to ensure that the glaze
is melted all the way through.
- You may be able to dig the sample out unbroken without damaging the firebrick, but I
usually fail. With a hacksaw, remove excess firebrick, the carefully break away the
remaining clay and alumina to reveal the sample.
- Trim the sample to the precise size required for the dilatometer with a diamond saw.
- Mount it in the dilatometer sample holder.
- Program the dilatometer controller for the desired temperature range.
- Using the temperature range over which the expansion is reasonably linear,
calculate the average expansion.
John Sankey 2008
| |
Measuring glaze expansion
 cut a hole in firebrick with a carbide tool
cut a hole in firebrick with a carbide tool
 line it with clay
line it with clay
 line the hole with alumina
line the hole with alumina
 fill with glaze and fire
fill with glaze and fire
 remove brick
remove brick
 sample ready for trimming
sample ready for trimming
 a sample in the trimmer
a sample in the trimmer
 the sample holder and dilatometer controller
the sample holder and dilatometer controller
 the dilatometer furnaces
the dilatometer furnaces
 the plot of expansion
the plot of expansion
photos by John Sankey and Ron Roy
|
 It is generally believed that the expansion for a stable glaze must be 1-10% less than
that of the clay. Glaze expansions much less than this can result in shivering - the
breaking off of sharp pieces of glaze under thermal stress. Glaze expansions higher
than that of the clay can cause crazing - fine cracks in the glaze surface that will
trap contaminants, thus making the item unsuitable for containing food.
It is generally believed that the expansion for a stable glaze must be 1-10% less than
that of the clay. Glaze expansions much less than this can result in shivering - the
breaking off of sharp pieces of glaze under thermal stress. Glaze expansions higher
than that of the clay can cause crazing - fine cracks in the glaze surface that will
trap contaminants, thus making the item unsuitable for containing food.
 Appen molar formulae for the variable expansion oxides:
Appen molar formulae for the variable expansion oxides:
 cut a hole in firebrick with a carbide tool
cut a hole in firebrick with a carbide tool
 line it with clay
line it with clay
 line the hole with alumina
line the hole with alumina
 fill with glaze and fire
fill with glaze and fire
 remove brick
remove brick
 sample ready for trimming
sample ready for trimming
 a sample in the trimmer
a sample in the trimmer
 the sample holder and dilatometer controller
the sample holder and dilatometer controller
 the dilatometer furnaces
the dilatometer furnaces
 the plot of expansion
the plot of expansion